学离散数学

复习一下离散数学。使用屈婉玲、耿素云、张立昂所著的离散数学（第2版），搭配BIT2021级这次考试的考纲和老师的PPT中隐含的侧重点进行知识点梳理。

本文仅供个人复习使用，严禁传播！

数理逻辑

命题逻辑的基本概念

命题：非真既假的陈述句。

真值：对于命题真假的判断结果（真/假）。真值为真的命题为真命题，反之为假命题。

简单命题/原子命题：不能被分解成更简单的命题。

复合命题：通过联结词联结而成的命题。

悖论：不能为真也不能为假的陈述句，不是命题。

p的否定式：复合命题“非p”或“p的否定”，记作\(\neg p\)。规定\(\neg p\)与p的真值始终取反。

p、q的合取式：复合命题“p并且q”，记作\(p \wedge q\)。规定p、q都为真的时候为真，否则为假。

p、q的析取式：复合命题“p或q”，记作\(p \vee q\)。规定p、q都为假的时候为假，否则为真。

p、q的蕴含式：复合命题“如果p，则q”，记作\(p \to q\)。规定p为真且q为假的时候为假，否则为真。称p为蕴含式的前件，q为后件。在逻辑关系中p是q的充分非必要条件，q是p的必要非充分条件。

p、q的等价式：复合命题“p当且仅当q”，记作\(p\leftrightarrow q\)。规定p、q真值相同的时候为真，反之为假。

简单命题/原子命题/命题常项/命题常元：基本单位，真值是确定的。

命题变项/命题变元：用p、q、r等表示真值可以变化的陈述句，不是命题。

合式公式/命题公式/命题形式/公式：单个命题变项或者多个联结而成的式子

子公式：公式中的一部分公式。

元语言符号：表示公式的大写字母。

对象语言符号：公式的具体内容。

公式的层次：

赋值/解释：给公式中的所有命题变项指定一个真值。如果使公式值为1，则称这个赋值为成真赋值，否则称为成假赋值。

真值表：将命题公式A在所有赋值下取值的情况列成表，称作A的真值表。

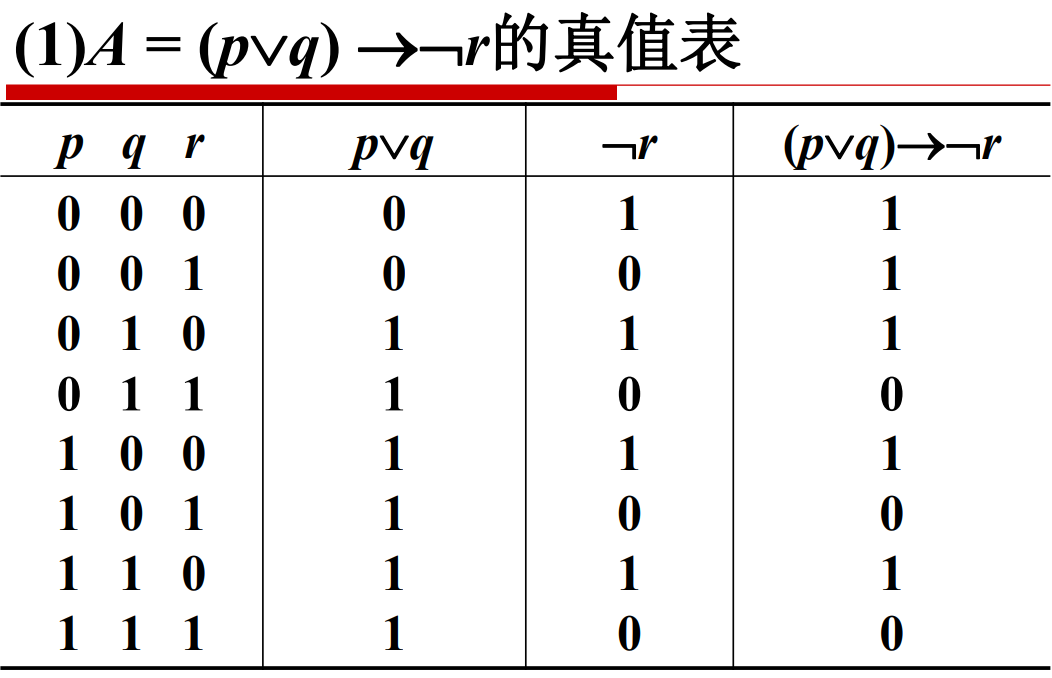
重言式/永真式：公式在各种赋值下取值均为真。

矛盾式/永假式：公式在各种赋值下取值均为假。

可满足式：公式不是矛盾式。（所以重言式也是可满足式）

哑元：对取值无影响的命题变项。

命题逻辑等值演算

等值式：若等价式\(A\leftrightarrow B\)是重言式（A和B真值表相同），则称A与B等值，记作\(A\Leftrightarrow B\)。这个符号不是联结词，而是元语言符号。

基本等值式：

代入实例：对基本等值式的具体运用。

等值演算：由已知等值式推演出另外一些等值式的过程。

置换规则：把两个等值式带入到相同的式子中去依然等值。

对偶式：

文字：命题变项及其否定。

简单析取式、简单合取式：仅由有限个文字构成的析取式、合取式。

析取范式、合取范式：由有限个简单合取式的析取、由有限个简单析取式的合取构成的命题公式。统称范式。

范式值定定理：一个简单析取式是重言式当且仅当它同时含有某个命题变项和它的否定式，一个简单合取式是矛盾式当且仅当它同时含有某个命题变项和它的否定式。

范式存在定理：任一命题公式都存在与之等值的析取范式与合取范式。

求公式A范式的步骤：

极小项（极大项）：在含有n个命题变项的简单合取式（简单析取式）中，若每个命题变项均以文字的形式在其中出现且仅出现一次，而且第i个文字出现在左起第i位上。

如果令否定式为0（1），单个命题变项为1（0），那么极小项（极大项）的排列组合可以组成不同的01串，每个排列组合的成真赋值（成假赋值）均只有一个，且为那个对应的01串，用串对应的十进制数i为这些排列组合编号，记为\(m_{i}\)（\(M_{i}\)）。

极大项与极小项的等值定理：\(\neg m_{i} \Leftrightarrow M_{i}, \neg M_{i} \Leftrightarrow m_{i}\)。

主析取范式（主合取范式）：所有简单合取式（简单析取式）都是极小项（极大项）的析取范式（合取范式）。

主范式存在定理：任何命题公式都存在与之等值的主析取范式和主合取范式，并且是唯一的。

主范式的求法：真值表法，通过真值表的成真赋值或成假赋值找到对应的极小项或极大项写出主范式；等值演算法，通过等值演算推到变形成主范式。

n元真值函数：\(F:\{0,1\}^{n} \rightarrow\{0,1\}\)，包含\(2^{n}\)个长为n的01串。

任何一个含n个命题变项的命题公式A都对应惟一的一个n元真值函数 F , F 恰好为A的真值表。

p、q的与非式：复合命题“p并且q的否定”，记作\(p \uparrow q\)，当p和q全为真的时候为假，否则为真，\(p \uparrow q \Leftrightarrow \neg(p \wedge q)\)。

p、q的或非式：复合命题“p或者q的否定”，记作\(p \downarrow q\)，当p和q有一个为真的时候为假，否则为真，\(p \downarrow q \Leftrightarrow \neg(p \vee q)\)。

p、q的不可兼析取：复合命题“非p当且仅当q”，记作\(p \bar{\vee} q\)，当p和q不同的时候为真，相同的时候为假，\(p \bar{\vee} q \Leftrightarrow \neg(p \leftrightarrow q)\)。

联结词完备集：设S是一个联结词集合，如果任何n(n不小于1)元真值函数都可以由仅含S中的联结词构成的公式表示，则称S是联结词完备集。

联结词完备集定理：\(S=\{\neg, \wedge, \vee\}\)是联结词完备集。

最小联结词完备集：S是联结词完备集，从S中任意去掉一个联结词后, 得到一个联结词集合S’, 至少有一个公式B,不等值于仅包含S’中联结词的任一公式, 则称S为最小联结词完备集。

与非或非完备集定理：{↑}，{↓}都是联结词完备集。

空简单析取式：不含任何文字的简单析取式，记作\(\lambda\)。

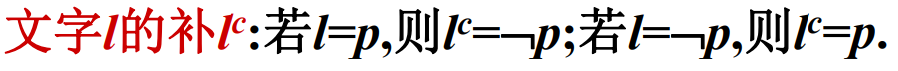
约定：简单析取式不同时含某个命题变项和它的否定,否则它为重言式,可以把它从合取范式中消去。

消解定理：

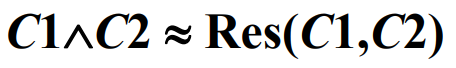
注意：这里仅仅是可满足性相同，不一定等值。

消解否证定理：一个合取范式是不可满足的当且仅当它有否证。

消解算法：

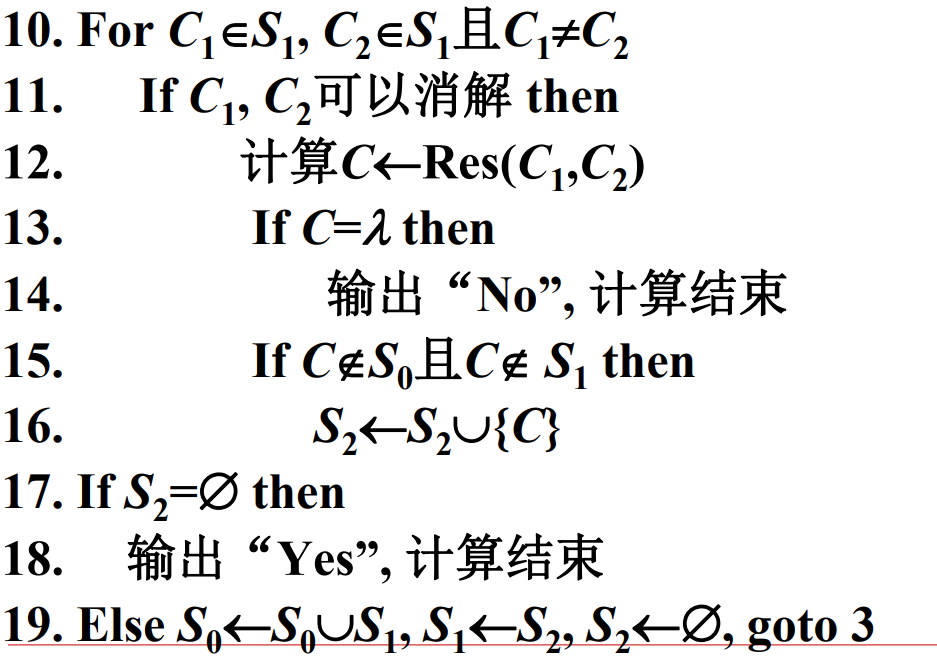
命题逻辑的推论理论

前提：已知的命题公式集合。

结论：从前提出发应用推理规则推出的命题公式。

推理：从前提出发推出结论的思维过程。

说明：推理是否正确与前提的排列次序无关，前提是一个有限的公式集合。设前提为集合\(\Gamma\)，将由前提推出B的推理记为\(\Gamma \vdash B\)。若推理是正确的，则记为\(\Gamma \models B\)，否则记为\(\Gamma \not\models B\)。这里称\(\Gamma \vdash B\)为推理的形式结构。

前提和结论是蕴涵关系，这个蕴含式为真推理就正确，否则就错误。推理正确并不能保证B一定成立，因为前提可能就不成立。

推理正确定理：由前提推理结论正确当且仅当前提→结论为重言式，→记作\(\Rightarrow\)。

推理正确定理中也表达了一种推理的形式结构。

判断推理是否正确的方法：真值表法、等值演算法、主析取范式法。

真值表法：

推理定律：

证明：描述推理过程的命题公式序列。

一个形式系统I由下面四部分组成：

（1）非空的字母表A(I)。

（2）A(I)中符号构造的合式公式集，记作E(I)。

（3）E(I)中的一些特殊的公式组成的公理集，记作\(A_{x}(I)\)。

（4）推理规则集，记作R(I)。

I就记为这样的四元组，其中前两个是形式语言系统，后两个是形式演算系统。

形式系统一般分为两类，一类是自然推理系统，从任意给定的前提出发，应用系统中的推理规则进行推理演算，无公理集，最后得到结论；一类是公理推理系统，它只能从若干条给定的公理出发，应用系统中的推理规则进行推理运算，得到系统中的重言式，称为定理。这里只介绍前者。

自然推理系统P定义如下：

2. 合式公式

3. 推理规则

（1）前提引入规则：在证明的任何步骤都可以引入前提。

（2）结论引入规则：在证明的任何步骤所得到的结论都可以作为后继证明的前提。

（3）置换规则：在证明的人和步骤，命题公式中的子公式都可以用等值的公式置换，得到公式序列中的又一个公式。

然后，还有一些结合推理定律导出的推理规则。

证明合理性定理：设A是公式集合，B是一个公式。于是，从A证明出B的充要条件是B是A的有效结论。

说明：“推出矛盾”就是得出了一个矛盾式的结论。

一阶逻辑基本概念

一阶逻辑也称一阶谓词逻辑或谓词逻辑。

个体词：指所研究对象中可以独立存在的具体的或抽象的客体。将特定的个体词称作个体常项，一般用小写字母a、b、c等表示；将泛指的个体词称作个体变项，一般用x、y、z等表示，并称个体变项的取值范围为个体域（或称作论域）。个体域可以使有穷集合，也可以是无穷集合。有一个特殊的个体域，它是由宇宙间一切事物组成的，称作全总个体域。

谓词：用来刻画个体词性质及个体词之间相互关系的词。表示具体性质或关系的谓词称作谓词常项，表示抽象的或泛指的性质或关系的谓词称作谓词变项。谓词都用大写英文字母F、G、H等表示，根据上下文区分常项还是变项。含n个个体变项的谓词P称作n元谓词，记作P（x1，x2，…，xn）。一般n=1时表示性质，更多的话就表示关系。

0元谓词：不含个体变项，当该谓词为谓词常项时，就是一个命题。

量词：用来表示个体常项或变项之间的数量关系的词。

全称量词\(\forall\)：表达“对所有的”，“每一个”，“对任一个”，“任意的”，“凡”，“都”等。

存在量词\(\exists\)：表达“存在”，,”有的”，“ 有一个”，“至少有一个”，“有 一些”等。

特性谓词：用来从全总个体域框定范围的谓词，为了保持与自然语言一致的逻辑，全称量词通常作为蕴含式的前件，存在量词一般作为合取式的前件。

多个量词出现时，量词对变元的约束通常与量词的次序有关，量词的次序不能随意颠倒。对于命题中的多个量词，约定从左到右的次序读出。

一阶语言：用于一阶逻辑的形式语言，将自然语言中的命题符号化。

非逻辑符号：个体常项符号、函数符号和谓词符号。

逻辑符号：个体变项符号、量词符号、联结词符号和括号与逗号。

一阶语言的字母表：包括非逻辑符号和逻辑符号。

一阶语言的项：个体常项符号和个体变项符号，可定值函数（自变量被个体项填充的函数），有限次地使用前两条的结果。

一阶语言的合式公式/公式：

封闭的公式/闭式：设A是任意的公式，若A中不含自由出现的个体变项。

解释：指定公式中的个体域及个体常项符号、函数符号、谓词符号。

赋值：指定自由出现的个体变项。

闭式定理：闭式在任何解释下都是命题。

注意：不是闭式的公式在解释下可能是命题，也可能不是命题（因为自由变元的原因不能判断真假）。

若公式A在任何解释和该解释下的任何赋值下均为真, 则称A为永真式(逻辑有效式)。若A在任何解释和该解释的赋值下均为假, 则称A为矛盾式(永假式)。若至少有一个解释和该解释下的一个赋值使A为真, 则称A为可满足式。

说明：永真式为可满足式，但反之不为真；在一阶逻辑中，判断任意给定公式类型的问题是不可判定的，若说一阶逻辑是可判定的，就要求给出一个能行的方法，使得对任一公式都能判断是否是有效的。所谓能行的方法，乃是一个机械方法，可一步一步做下去，并在有穷步内实现判断。由于一阶逻辑中的永真(永假)公式，要求所有解释I都满足(弄假)该公式。而解释I依赖于一个非空集合D。由于集合D可以是无穷集合，而集合D的 “数目”也可能是无穷多个，因此，所谓公式的 “所有”解释，实际上是无法考虑的。

代换实例：

代换实例一致性定理：重言式的代换实例都是永真式，矛盾式的代换实例都是矛盾式。

一阶逻辑等值演算与推理

等值：设A, B是两个谓词公式, 如果\(A\leftrightarrow B\)是永真式, 则称A与B等值, 记作\(A\Leftrightarrow B\), 并称\(A\Leftrightarrow B\)是等值式。也就是说A与B等值要求在任何解释I下真值都相同。

基本等值式：

第一组：命题逻辑中16组基本等值式的代换实例。

第二组：

（1）消去量词等值式

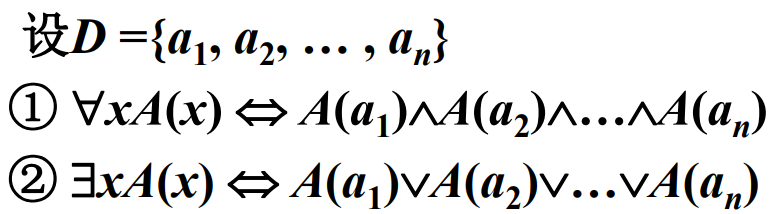
（2）量词否定等值式

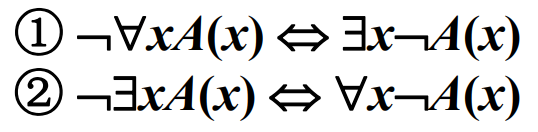
（3）量词辖域收缩与扩张等值式

（4）量词分配等值式

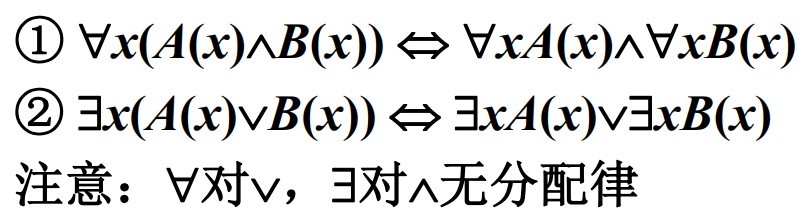
第三组：

置换规则

换名规则：设A为一公式，将A中某量词辖域中个体变项的所有约束出现及相应的指导变元换成该量词辖域中未曾出现过的个体变项符号，其余部分不变，设所得公式为A’，则\(A\Leftrightarrow A'\)。

代替规则：设A为一公式，将A中某个个体变项的所有自由出现用A中未曾出现过的个体变项符号代替，其余部分变，设所得公式为A’，则\(A\Leftrightarrow A'\)。

前束范式：

就是把量词都堆到前面。

前束范式存在定理：一阶逻辑中的任何公式都存在与之等值的前束范式。

Skolem范式：不做介绍，请看ch5PPT的第33页。

一阶逻辑推理的形式结构：

推理定理：永真式的蕴含式

第一组 命题逻辑推理定理的代换实例。

第二组 基本等值式生成的推理定理。

第三组 其他常用推理定律。

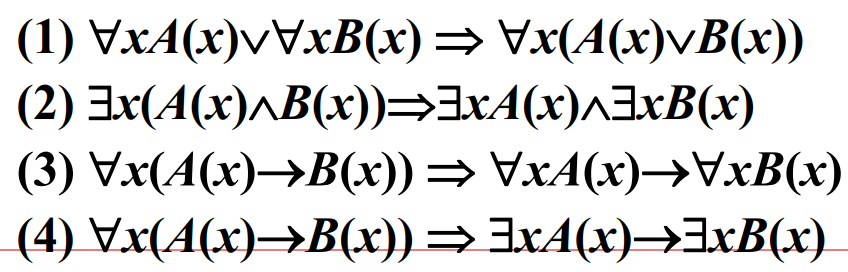
推理规则：

自然推理系统\(N_{\mathcal{L} }\)：

这里证明的格式与自然推理系统P相同。

集合论

集合代数

把一些事物会聚到一起组成一个整体就称作集合，而这些事物就是这个集合的元素或成员。

集合的元素是彼此不同的，无序的。

规定集合的元素都是集合，元素和集合之间的关系是隶属关系，即属于或不属于。

这里的集合有子集、真子集、空集、（被）包含、相等的概念。

空集定理：空集是一切集合的子集。

推论：空集是唯一的。

含有n个元素的集合简称为n元集，它的含有m个元素的子集称作它的m元子集。

基数（势）：集合 S 中不同元素的数目称为 S的基数或势记为|S|或#S。

|S|是有限的集合为有穷集合（无限为无穷集合）。

设A为集合，把A的全体子集构成的集合称作A的幂集，记作P(A)（或\(\mathcal{P}A,2^{A}\)）。

在一个具体问题中，如果所涉及的集合都是某个集合的子集，则称这个集合为全集，记为E。

最小的全集是所有集合的并集。全集具有相对性，与问题有关，不存在绝对的全集。

集合的基本运算：交、并、相对补、对称差、绝对补。

并和交可以推广到有穷个甚至无穷个集合上，称为广义并和广义交。

集合运算优先级：一类运算：广义并，广义交，幂集，绝对补，运算由右 向左进行。二类运算：初级运算交，并，相对补，对称差，优先顺序由括号确定。混合运算：一类运算优先于二类运算。

集合恒等式：

说明：只涉及一个运算的算律有：交换律、结合律、幂等律。涉及两个不同运算的算律：分配律、吸收率。涉及补运算的算律：德摩根律、双重否定律。涉及全集和空集的算律：补元律、零律、同一律、否定律。

集合证明题：命题演算法、等式置换法。见ch6PPT36页。

包含排斥原理：

欧拉函数：。

二元关系

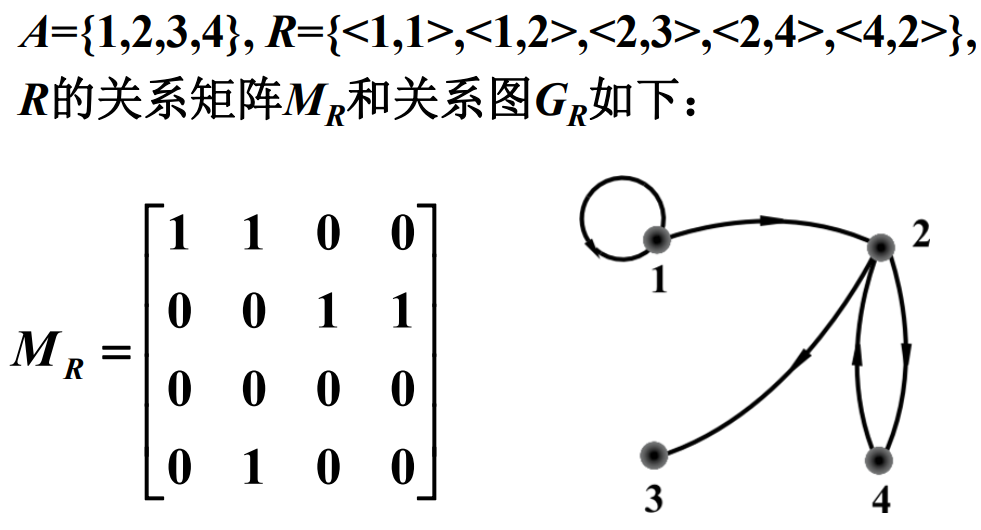
有序对：由两个元素 x 和 y，按照一定的顺序组成的二元组称为有序对，记作<x,y>。

有序对不等的元素交换顺序后与原有序对不等。

笛卡尔积：设A,B为集合，笛卡尔积记作A×B，\(A \times B=\{<x,y>\mid x \in A \wedge y \in B\}\)。读笛卡尔积时，一般表示是这种运算或运算后的集合。

两个集合有一个是空集，笛卡尔积就是空集。笛卡尔积不符合交换律和结合律，但是对于并或交运算满足分配律，笛卡尔积的基数等于两个集合的基数之积。

如果一个集合里的元素都是有序对或者一个集合为空，那么称这个集合为一个二元关系，简称为关系，记作R。显然的，关系是元素为有序对或为空的集合。

设A,B为集合, A×B的任何子集所定义的二元关系称为从A到B的二元关系,当A=B时则称为A上的二元关系。

设A为集合，空集是A上的关系，称为空关系。

几个常见关系：

关系的表示：

（1）几何表达式。

（2）关系矩阵

（3）关系图

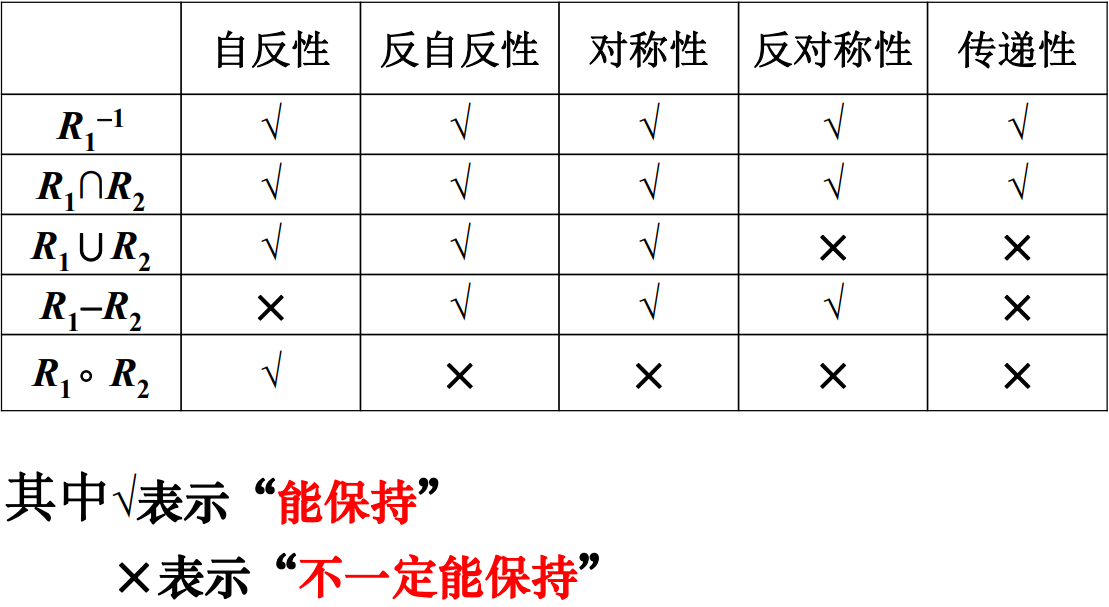
关系的集合运算：若R和S是从集合X到集合Y的两个关系，则R、S的并、交、补、差、对称差仍是X到Y的关系。

关系的定义域：\(dom R=\{x \mid \exists y(<x,y>\in R)\}\)，关系集合中的有序对的第一个元素组成的集合。

关系的值域：\(ran R=\{y \mid \exists x(<x,y>\in R)\}\)，关系集合中的有序对的第二个元素组成的集合。

关系的域：\(fld R=dom R \cup ran R\)，定义域和值域的并集。

关系的逆运算：把原关系集中的有序对顺序调转\(R^{-1}=\{<y,x>\mid<x,y>\in R\}\)。

关系的合成运算：给两个关系集合的有序对“首尾相接”，\(R \circ S=\{<x,z>\mid \exists y(<x,y>\in R \wedge<y,z>\in S)\}\)。

设R为二元关系，A是集合：

R在A上的限制记作\(R\lceil A\)，在这里R中的有序对只保留了第一个元素包含在集合A里的部分，也就是“限制定义域”。

A在R上的像记作R[A]，值为R在A上限制的值域。

关系逆定理：关系逆的逆等于本身，定义域的逆等于值域，值域的逆等于定义域。

关系算律：关系的合成运算是可结合的，关系的合成运算可以分配关系的逆运算。

恒等结合定理：关系与恒等关系左结合或又结合的结果还是关系本身。

关系运算对集合运算的分配：

关系的n次幂：

幂运算的算律：

对于关系图来说，xRy说明x到y有一条长度为1的有向路径，n次幂的话则是长度为n的有向路径。

幂循环定理：设 A 为 n 元集, R 是A上的关系, 则存在自然数 s 和 t, 使得R的s次幂和t次幂相等。

推论：

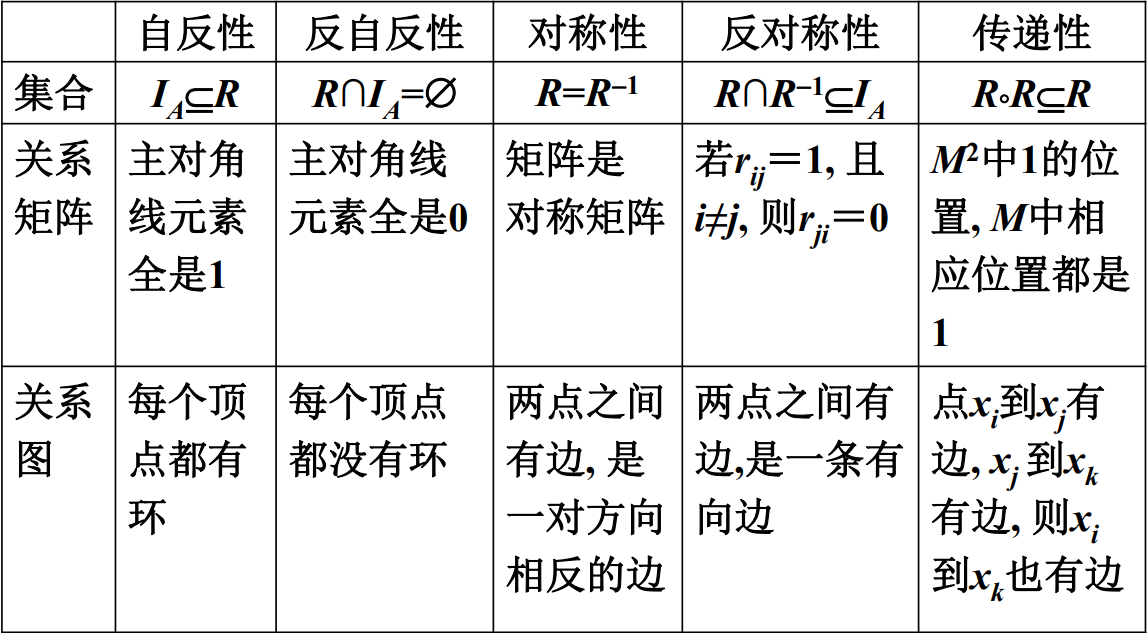
关系自反：。

在关系矩阵中对角线上的元素都是1，在关系图中每个节点都有自回路。

关系反自反：。

在关系矩阵中对角线上所有元素都是0，在关系图中任一节点均无自回路。

一个集合不是自反的，不一定就是反自反的。

关系对称：。

关系矩阵是对称的，在关系图中节点间若有边，必是往返两条。

关系反对称：。

关系矩阵处于对称位的元素不能同时为一（对角元除外），在关系图中两点间若有边，只能有一条。

一个关系是对称的，不一定是反对称的。

关系传递：。

在关系矩阵中rij=1，rjk=1，则rik=1，在关系图如果a可达b，那必有一条通路长度为1.

关系性质成立的充要条件：

总结：

闭包：设R是非空集合A上的关系, R的自反(对称或传递)闭包是A上的关系R’, 使得R’满足以下条件：R’是自反的(对称的或传递的)，R是R’的子集，对A上任何包含R的自反(对称或传递)关系R‘’有R’是R‘’的子集。换句话说，就是给关系集合添加最少的有序对，使其具有自反(对称或传递)特性。R的自反闭包记作r(R)，对称闭包记作s(R)，传递闭包记作t(R)。

闭包的求法：

加的时候不要出现2，不是0就是1。

Warshall算法求闭包：

闭包反判定理：R是自反的当且仅当 r(R)=R，R是对称的当且仅当 s(R)=R，R是传递的当且仅当 t(R)=R。

闭包子集不变定理：如果某个集合为另一集合的子集，那么他们的同种闭包也满足这种子集关系。

闭包特性保留定理：若R是自反的, 则 s(R) 与 t(R) 也是自反的，若R是对称的, 则 r(R) 与 t(R) 也是对称的，若R是传递的, 则 r(R) 是传递的。

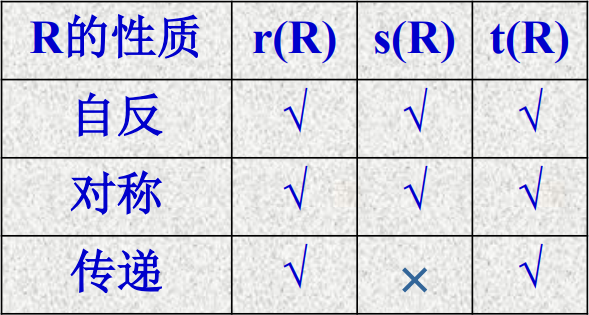
如果需要进行多个闭包运算，比如求R的自反、对称、传递的闭包，运算顺序如下：tsr(R) = rts(R) = trs(R)。

等价关系：自反、对称、传递的关系，若<x,y>是这个关系中的有序对，称x等价于y，记作x~y。

等价类：记作\([x]_{R}\)简记为[x]，成为x的等价类，是在等价关系R中与x有关系（同在一个有序对）的y的集合。

等价类定理：

商集：设 R 为非空集合A上的等价关系, 以 R 的所有等价类作为元素的集合称为A关于R的商集, 记做A/R。

商集的元素是集合。

覆盖：设A为非空集合, 若A的子集族π满足不含空集且全部并在一起等于A，称π为A的一个覆盖。

划分：覆盖π的元素中没有重叠，是覆盖的特殊情形。

最小划分：是由作为类的集合本身构成。

最大划分：是由包含单个元素的类组成。

商集划分定理：集合A上的一个等价关系R, 决定了A的一个划分，该划分就是商集 A/R 。

划分确定关系定理：集合A的一个划分,确定A的元素间的一个等价关系(a R b 当且仅当 a 和 b 在同一个分块中），划分和等价关系在本质上是相同的。

偏序关系：非空集合A上的自反、反对称和传递的关系，记作\(\preceq\)。设\(\preceq\)为偏序关系如果<x,y>属于\(\preceq\)，则记作\(x\preceq y\)，读作x“小于等于”y。

可比：x与y可比当且仅当\(x\preceq y \wedge y\preceq x\)。大于小于或等于，x与y是不可比的。

全序（或线序）：偏序关系域中全部元素都互相可比。

覆盖：

集合A和A上的偏序关系≼一起叫做偏序集, 记作<A,≼>。

哈斯图：利用偏序关系的自反、反对称、传递性进行简化的关系图，省去自回路，省略箭头，下小上大，省略跨越边。

最大元和最小元没有并列者，极大元和极小元有并列者。

对于有穷集，极小元和极大元一定存在，可能存在多个。最小元和最大元不一定存在，如果存在一定惟一。最小元一定是极小元；最大元一定是极大元。孤立结点既是极小元，也是极大元。

上界下界和最大元最小元的区别在于y的定义域，在上界下界这里，y是属于大集合的，所以不一定在B中。如果C和D中没有最元，那么上确界和下确界是没有的。

下界、上界、下确界、上确界不一定存在，下界、上界存在不一定惟一，下确界、上确界如果存在，则惟一，集合的最小元是其下确界，最大元是其上确界，反之不对。

函数

设F为二元关系，若任意定义域中的x都有唯一值域中的y使xFy成立，则称F为函数。也就是说，这里的函数是二元关系，是集合。

对于函数F, 如果有 xFy, 则记作 y=F(x), 并称 y 为F 在 x的值。

如果两个函数F和G相等\(F=G \Leftrightarrow F \subseteq G \wedge G \subseteq F\)，一定满足：domF=domG，即定义域相等；任何x属于domF=domG都有F(x)=G(x)，即函数值相等。

设A, B为集合, 如果f 为函数,\(dom f=A, ran f \subseteq B\)，则称 f 为从A到B的函数, 记作 f：A→B。

所有从A到B的函数的集合记作\(B^{A}\)，符号化表示为\(B^{A}=\{f\mid f:A\to B\}\)。

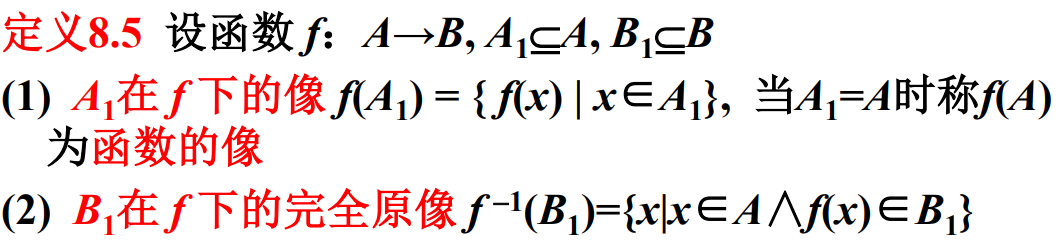
像是值域的子集。某集合像的完全原像不一定等于该集合，但该集合是像的完全原像的子集（因为有函数值相同的情况）。

设f：A→B，

函数满射：值域等于B。

单射函数：每一个y存在唯一的x，一夫一妻。

函数双射：既是单射的又是满射的。

常函数：对于所有的x函数值都是常数c。

恒等函数：所有x的函数都等于x，是一个恒等关系。

类似的也可以定义单调递减和严格单调递减的函数。

特征函数：

自然映射：

设R为A上等价关系，称 g 是从 A 到商集 A/R 的自然映射。

复合函数基本定理：

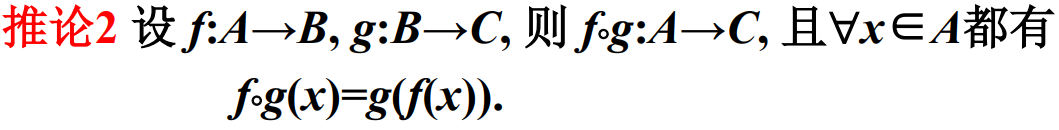
复合函数性质定理：

注意：定理的逆命题不一定为真。

恒等复合定理：设 f : A→B, 则\(f=f^{\circ} I_{B}=I_{A}{ }^{\circ} f\)。

反函数存在条件：

反函数双射定理：

对于双射函数f:A→B，称B→A是它的反函数。

反函数归中定理：

集合等势：存在两集合之间的双射函数，记作\(A\approx B\)，如果AB不等势，记作\(A\not\approx B\)。

等势等价定理：

等势的重要结果：\(N\approx Z\approx Q\approx N\times N\)，任何实数区间都于实数集合R等势。

康托定理：自然数与实数集不等势，任何集合与它的幂集都不等势。

设A, B是集合, 如果存在从A到B的单射函数,就称B优势于A, 记作\(A \leqslant \cdot B\)。如果B不是优势于A，则记作\(A \not \leqslant \cdot B\)。

如果满足优势关系，且不是满射（双射），也就是不等势，就是真优势。

优势性质定理：

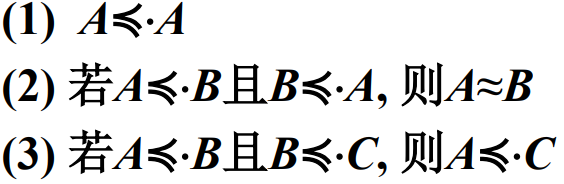
a的后继：

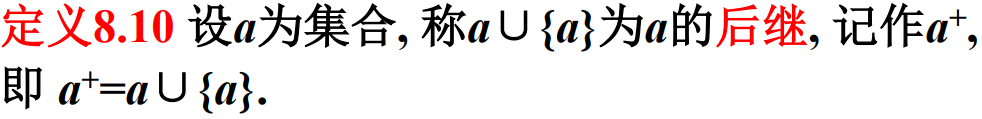
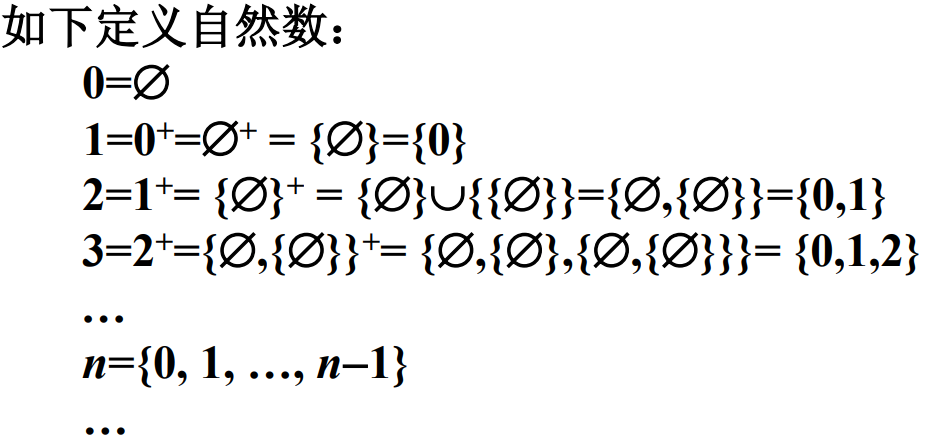
有穷集合：它与某个自然数等势。

无穷集合：不是又穷的集合。

基数：

关于基数的大小，就是先是自然数0,1,2……再是阿列夫0，阿列夫1，后面还有更大的基数，比如实数的幂集的基数，不过我们知道，阿列夫零和阿列夫1之间是没有其它基数的。

可数集/可列集：基数不大于阿列夫0的集合，自然数集是基数最大的可数集。

可数集的性质：

代数结构

代数系统

二元运算：f:S×S→S称为S上的二元运算。要求集合中的任何两个元素都可以进行这种运算，且运算的结果是唯一的。除此之外，运算的结果应属于S，即运算时封闭的。

一元运算：f:S→S称为S上的一元运算，简称一元运算，可以看出，一元运算可以用关系表示。

算符：

表示二元或一元运算的方法：解析公式和运算表。

如果二元运算可交换，则满足交换律；如果可结合，则满足结合律；如果次幂相等，则满足幂等律。

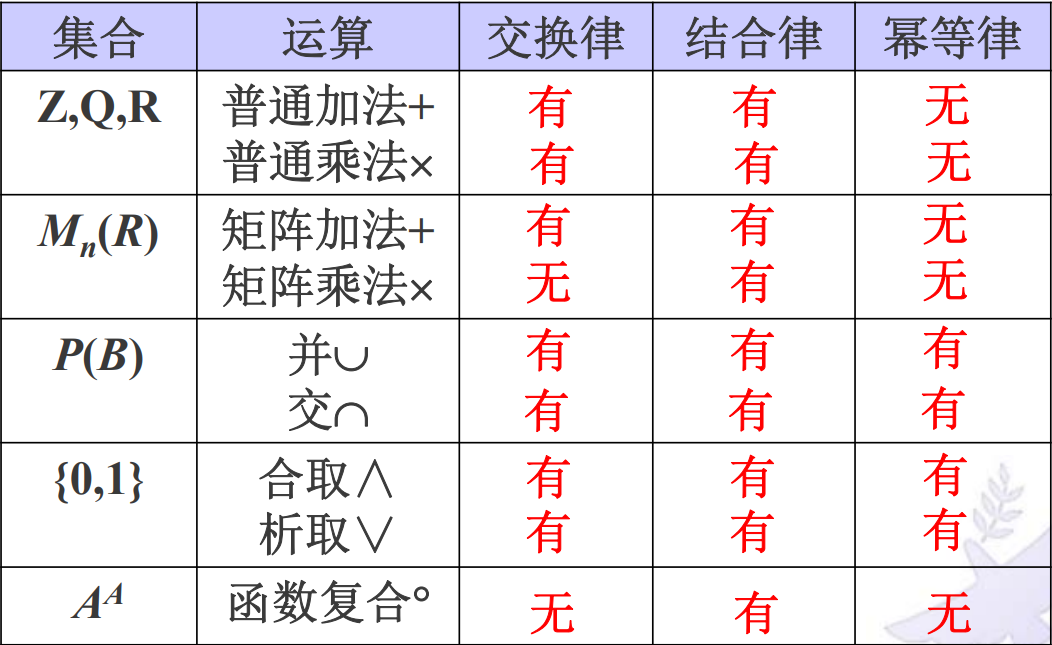
如果S上有两个不同的二元运算，可以分配，就像加法和乘法一样，就说乘法运算对加法运算满足分配律；如果这两个运算都可交换，而且满足x@(x#y)=x，x#(x@y)=x，则称这两个运算满足吸收率。

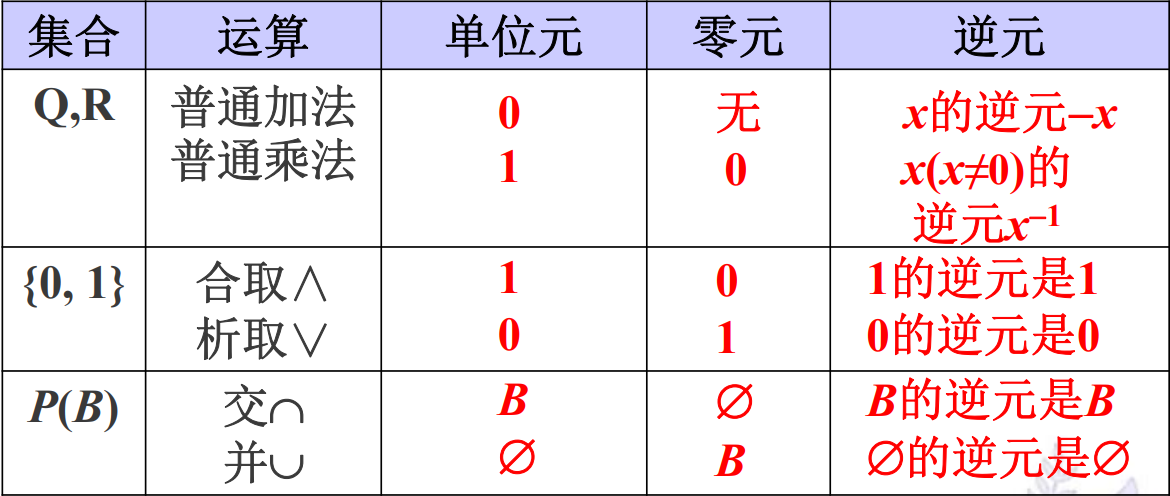
单位元：进行运算不改变另一元素的值的元素，分为左单位元和右单位元，取决于其在二元运算中实现单位运算效果所处的位置。如果既是左单位元又是右单位元，那么就称其为单位元，也叫幺元。

0是加法单位元，1是乘法单位元。

零元：对任何元素进行二元运算都得零元本身，也分左零元和右零元，又是左零元又是右零元就叫它零元了。

0是乘法零元，加法没有零元。

逆元：

加法逆元是相反数，乘法逆元是倒数。

有幺元：该元素所对应的行和列依次与运算表的行和列相一致。

有零元：该元素所对应的行和列中的元素都与该元素相同。

逆元：设 A 中有幺元，a 和 b 互逆，当且仅当位于 a 所在行，b 所在列的元素以及 b 所在行，a 所在列元素都是幺元。

唯一性定理：如果既有左单位元又有右单位元，那么左单位元等于右单位元，该元素为该运算中唯一的单位元；如果既有左零元又有右零元，那么左零元等于右零元，该元素为该运算中唯一的零元。如果运算所属集合的基数大于一，那么单位元和零元不相等。如果既有左逆元，又有右逆元，那么左逆元灯源右逆元，为唯一逆元。

代数系统/代数：

构成代数系统的成分：集合（也叫载体，规定了参与运算的元素），运算（这里只讨论有限个二元和一元运算），代数常数（通常是与运算相关的特异元素：如单位元等）。

代数常数：研究代数系统时，如果把运算具有它的特异元素也作为系统的性质之一，那么这些特异元素可以作为系统的成分。

同类型的代数系统：两个代数系统中运算的个数相同，对应运算的元数相同，且代数常数的个数也相同。

注意：个数相同就行。

子代数系统/子代数：

也就是参与运算的域是原来的子集了。

最大的子代数：本身。

最小的子代数：如果令V中所有代数常数构成的集合是B，且B对V中所有的运算都是封闭的，则B就构成了V的最小的子代数。

最大和最小的子代数称为V 的平凡的子代数。

若B是S的真子集，则B构成的子代数称为V的真子代数。

积代数：

注意：积代数的定义可以推广到具有多个运算的同类型的代数系统。

积代数的性质定理：

同态映射/同态：

同态是指那个函数f。

单同态：f是单射

满同态：f是满射，两边一个元素都不浪费，这时称V2是V1的同态像， 记作V1~V2。

同构：f是双射，一一对应，记作\(V_{1}\cong V_{2}\)。

自同态：V1=V2。

群与环

半群：只有一个可结合的二元运算的代数系统V。

幺半群/独异点：有单位元的半群V。

群：有逆元的幺半群，有单位元和逆元的半群，只有一个可结合的二元运算且有单位元和逆元的代数系统，通常记为G。

Klein四元群：见ch10.1-2PPT29页。

若群G是有穷集，则称G是有限群，否则称为无限群。（这里指的是G中的集合，因为代数系统是一个集合和一堆运算组成的系统）

群G 的基数称为群 G 的阶，有限群G的阶记作|G|。（这里说的也是那个集合）

只含单位元的群称为平凡群。

若群G中的二元运算是可交换的，则称G为交换群或阿贝尔(Abel) 群。

群中元素的幂：

元素的阶：

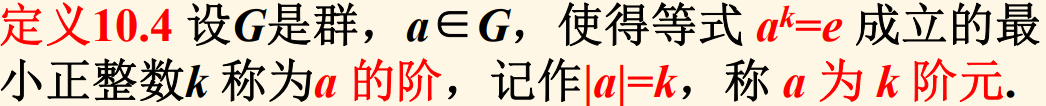
若不存在这样的正整数 k，则称 a 为无限阶元。

群的性质：幂运算规则定理：

元素的阶的性质定理：

群的消去律定理：G为群，则G中适合消去律，即对任意a, b, c属于G中集合，有若ab=ac则b=c；若ba=ca，则b=c。

方程解唯一定理：对于群G中任意a，b，方程ax=b和ya=b在G中有解且仅有惟一解。

无零元定理：群中不可能有零元。

子群：

子群判定定理1：设G为群，H是G的非空子集，则H是G的子群当且仅当H中的任意a，b经过运算还在H中，H中任意a的逆元还在H中。

子群判定定理2：设G为群，H是G的非空有穷子集，则H是G的子群当且仅当H中的任意a，b经过运算还在H中。

子群判定定理3：设G为群，H是G的非空子集，则H是G的子群当且仅当任取H中a，b\(ab^{-1}\in H\)。

生成子群：

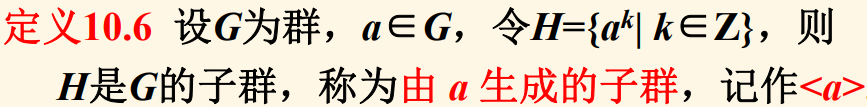
群G的中心：所有可交换的元素构成的子群，记为C。

子群的交与并：

子群格：

就是由所有子群构成的偏序关系集合。

陪集：

陪集是子群的陪集，代表元素是原群中的元素。

陪集的基本性质定理：

这个中括号是等价类的意思，是一个包含所有等价元素的集合。

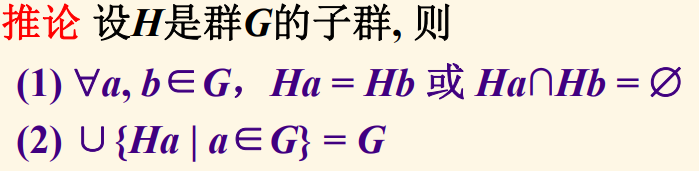
对于左陪集呢：

正规子群：对于任意a属于G，Ha=aH，称H为正规子群，也称为不变子群。

H的左陪集的数量和右陪集的数量相同。

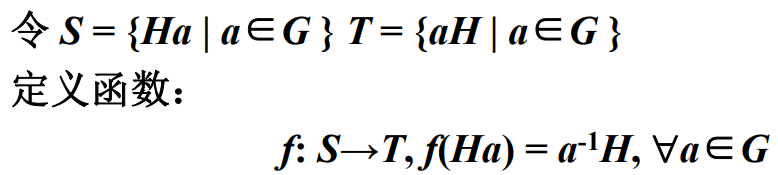
显然f是S到T的双射函数。

H在G中的不同右陪集(或左陪集) 数，称为H在G 中的指数，记为[G:H]。

Lagrange定理：设G是有限群，H是G的子群，则|G| = |H|·[G:H]。即子群的阶整除群的阶。

推论1：设G是n阶群，则\(\forall a\in G\)，|a|是n的因子，\(a^{n}=e\)。

推论2：对阶为素数的群G，必存在a∈G使得G =<a>。

注意：Lagrange定理的逆命题不为真。

如果群G只含1阶元和2阶元，则G是Abel群（交换群）。

循环群和生成元：

循环群的分类：

任何一个循环群必定是Abel群。

生成元定理：

欧拉函数：比n小且与n互质的正整数的个数。

循环群的子群定理：G的子群仍是循环群；若G=<a>是无限循环群，则G的子群除{e}以外都是无限循环群；若G=<a>是n阶循环群，则对n的每个正因子d，G恰好含有一个d 阶子群。

最小正方幂元：

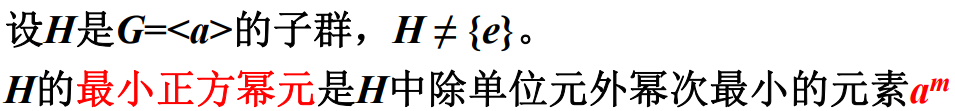
求循环群所有子群的方法：

置换：

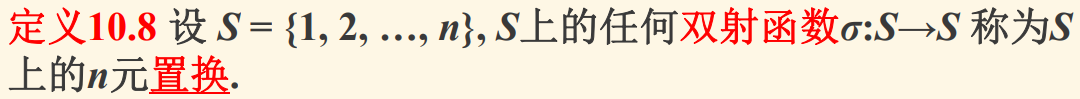
把群中集合的元素做双射变换。

置换性定理：群<G,*>的运算表中的每一行或每一列都是 G 的元素的一个置换。

置换的乘法：设σ, τ是n元置换, σ和τ的复合σ ∘τ 也是n元置换, 称为σ与τ 的乘积, 记作στ。

轮换：

对换：k=2的轮换。

轮换分解式：

轮换分解式的特征定理：

说明：通常省略轮换分解式中的1阶轮换，如果其中全是1阶轮换，则需要保留一个1阶轮换。如恒等置换(1)(2)(3)(4)(5)简记为(1)。根据函数复合的性质，交换轮换的次序后得到的n元置换是相等的。
(1 8 3 4 2) (5 6 7) = (5 6 7) (1 8 3 4 2)

置换的对换分解：

对换分解的特征：对换分解式中对换之间可以有交，分解式也不惟一。如果n元置换σ可以表示成奇数个对换之积，则称σ为奇置换，否则称为偶置换。表示式中所含对换个数的奇偶性是不变的。可以证明n元置换中奇置换和偶置换各有n!/2个。

n元及置换和偶置换的数量相等。

n元对称群：所有的 n元置换构成的集合Sn关于置换乘法构成群。

n元置换群：n元对称群的子群。

n元交错群：设An是所有的n元偶置换的集合，则An是n元对称群Sn的子群，称为n元交错群。

Polya定理：

环：设<R,+,·>是代数系统，+和·是二元运算，如果满足：<R,+>构成交换群，<R,·>构成半群，·运算关于+运算适合分配率。则称<R,+,·>是一个环。

说明：通常称+运算为环中的加法；·运算为环中的乘法, 通常可以省略。环中加法单位元记作 0，乘法单位元(若存在)记作1。对任何元素 x，称 x 的加法逆元为负元，记作-x, (x-y)表示x+(-y). 若 x 存在乘法逆元的话，则称之为逆元，记作\(x^{-1}\)。nx表示n个x相加，\(x^{n}\)表示n个x相乘。

环的运算性质定理：

交换环：环中的乘法适合交换律。

含幺环：环中的乘法存在单位元。

无零因子环：\(\forall a, b \in R, \quad a b=0 \Rightarrow a=0 \vee b=0\)。

整环：R既是交换环，又是含幺环和无零因子环。

域：

无零因子环判定定理：在环<A,+,·>中无零因子当且仅当乘法满足消去律， 即对于c≠0和c∙a=c∙b,必有a=b。

格与布尔代数

格：设S和S上的偏序关系构成偏序集，如果S中任意两个元素都有最小上界和最大下界，则称S关于偏序作成一个格。

可以把求{x, y} 最小上界x∨y和最大下界x∧y看成 x 与 y 的二元运算∨和∧。

通常把在偏序关系的基础上定义的格称为偏序格。

常见的格有幂集格、子群格等。

由B生成的子群：

格的对偶命题：设 f 是含有格中元素以及符号 =,≼ ,≽ ,∨和∧的命题。令 f是将 f 中的≼替换成≽,≽替换成≼,∨替换成∧,∧替换成∨ 所得到的命题。称 f 为 f 的对偶命题。

格的对偶原理：设 f 是含有格中元素以及符号=,≼,≽,∨和∧等的命题。 若 f 对一切格为真, 则 f 的对偶命题 f*也对一切格为真。

格中的基本的不等式和等式：

格的算律：

格作为代数系统的定义：设<S,*,◦>是具有两个二元运算的代数系统, 若对于∗ 和◦运算适合交换律、结合律、吸收律, 则可以适当定义S中的 偏序 ≼,使得<S,≼>构成格, 且任取a, b∈S 有 a∧b = a∗b, a∨b = a◦b。

设<S,*,◦>是代数系统, ∗和◦是二元运算, 如果∗和◦ 满足交换律、结合律和吸收律, 则<S,*,◦>构成格。（格的一个 等价定义）

通常把由代数系统定义的格称为代数格。

等价格定理：偏序格和代数格是等价的。

所以没有区分代数格和偏序格的必要，统称为格即可。

格的序关系与运算定理：设L是格, 则任取a, b∈L有a ≼ b \(\Leftrightarrow\) a∧b = a\(\Leftrightarrow\) a∨b = b。

格的保序定理：设L是格, 任取a, b, c, d∈L，若a ≼ b 且 c ≼ d, 则a∧c ≼ b∧d, a∨c ≼ b∨d。

子格：

格的同态：

分配格：设<L,∧,∨>是格, 若任取a,b,c∈L,有a∧(b∨c) = (a∧b)∨(a∧c) ，a∨(b∧c) = (a∨b)∧(a∨c) 则称L为分配格。

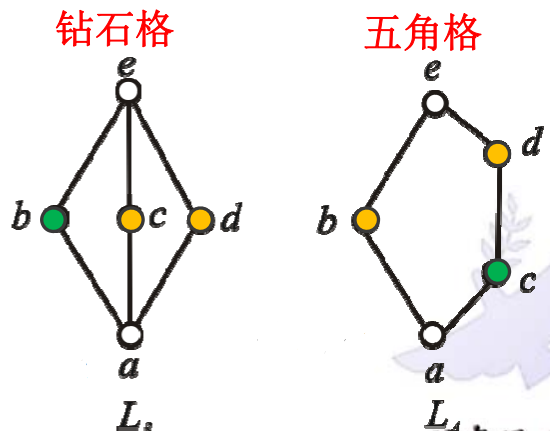
分配格判定定理：设L是格, 则L是分配格当且仅当L不含有与钻石格或五角格同构的子格。

推论：小于五元的格都是分配格，任何一条链都是分配格。

全上界和全下界：

说明：格L若存在全下界或全上界, 一定是唯一的。一般将格L的全下界记为0, 全上界记为1。

有界格：设L是格, 若L存在全下界和全上界, 则称L 为有界格, 一般将有界格L记为<L,∧,∨, 0, 1>。

有界格性质定理：

说明：0是关于∧运算的零元,∨运算的单位元；1是关于∨运算的零元,∧运算的单位元。

注意：对于涉及到有界格的命题, 如果其中含有全下界0或全上界1, 在求该命题的对偶命题时, 必须将0替换成1, 而将1替换成0。

有界格中的补元：

说明：若b是a的补元, 那么a也是b的补元。a和b互为补元。

有界分配格补元唯一性定理：设<L,∧,∨, 0, 1>是有界分配格. 若L中元素 a 存在补 元b, 则b是a唯一的补元。

有补格：设<L,∧,∨, 0, 1>是有界格, 若L中所有元素都有补元存在, 则称L为有补格。

布尔格/布尔代数：如果一个格是有补分配格, 则称它为布尔格或布尔代数。记为<B,∧,∨,', 0, 1>，’是求补运算。

集合代数：幂集格<P(B), ∩,∪, ~, 空集符号 , B>,构成布尔代数，称为集合代数。

布尔代数性质定理：

布尔代数作为代数系统的定义：

说明：布尔代数的两种定义是等价的。布尔代数的性质很多。上面四条算律能推出结合律、吸收律，而满足格定义；还可以推出幂等律、双重否定律、德摩根律等。

原子：

有限布尔代数的表示定理：设B是有限布尔代数, A是B的全体原子构成的集合, 则B同构于A的幂集代数P(A)。

推论1：任何有限布尔代数的基数为2的n次方, n∈N。

推论2：任何等势的有限布尔代数都是同构的。

图论

图的基本概念

多重集合是元素可以重复出现的集合。

重复度是元素在多重集合中出现的次数。

无序对是两个元素构成的集合，因为是集合，所以顺序是无意义的，这一点与尖括号表示的有序对相反。

无序积是\(A \& B=\{(x, y) \mid x \in A \wedge y \in B\}\)

一个图是由一些结点和连接两结点间的连线组成,至于连线的长短、曲直及结点的位置是无关紧要的，也就是说我们只考虑其逻辑关系。

无向图(Graph)是一个有序的二元组\(G=<V, E>\)，V 为非空有穷集，称为顶点集，其元素称为顶点(vertex)或者结点(node)。E为无序积V&V的有穷多重子集，其元素称为无向边，简称边(edge)。

有向图(Digraph)是一个有序的二元组\(D=<V, E>\)，V和无向图是一样的，E是V×V的多重子集，称为边集, 其元素称为有向边，简称边(edge/arc)。有时用V(D)和E(D)分别表示V和E。

无向边和有向边分别与无向图和有向图的节点无序对和节点有序对相关联，对于有向边，有序对的第一个元素代表始点，后一个元素代表终点。

还有一种图叫做混合图，有一些边是有向边，有一些边是无向边，今后这里只讨论有向图和无向图。

可用G泛指图（用G表示无向图，D表示有向图），用|V(G)|，|E(G)|分别表示G的顶点数和边数。用|V(D)|，|E(D)|分别表示D的顶点数和边数。

n阶图为n个顶点的图。

零图为边数为0的图，也就是仅由孤立点组恒的图。

平凡图是1阶零图，就是一个点。

空图就是啥也没有，\(\emptyset\)。

标定图就是每个顶点和边都有指定符号的图。

有向图的基图就是把这个有向图的方向全部去掉所变成的无向图。

边与某两个点关联意味着该边连接着这两个点。边关联的两个顶点称为这个边的端点。

如果一条边关联了同一个点，那么称这条边为环。

无边关联的点被称作孤立点。

这条边连了这个点几次，就称这个边与这个点的关联次数是几。（显而易见的，没关系的话关联次数为0）

如果两个点有一条边相连，那么就称这两个点相邻接，如果是有向图，那么说始点邻接到终点，终点邻接于始点。

如果两条边至少有一个公共端点，就称这两条边相邻接，在有向图中，一条边的终点是另一条边的始点，则称这两条边相邻，也就是说两条边的方向需要一顺。

一个点的邻域是与这个点相邻的所有点组成的集合，若该集合加上这个点自身，被称作闭邻域。

一个点的关联集是与这个顶点相关联的所有边构成的集合。

对于有向图来说，一个点的后继元集\(\Gamma_{D}^{+}(v)\)，是以这个点为始点的边的所有终点的集合。一个点的先驱元集\(\Gamma_{D}^{-}(v)\)，是一这个点为终点的边所有始点的集合。

注意：有向图顶点的邻域包含了通过两种边相关联的点。

平行边：对于无向图来说，就是关联于统一定点的边多余一条，这些边就是平行边，对于有向图来说，还要方向相同。

重数：平行边的条数。

多重图：含有平行边的图。

简单图：不含平行边和环的图，是一种对边的双重约束。

点v的度数d(v):v作为边的短点的次数之和（这样，环一次就可以贡献2度）。

悬挂顶点：度数唯一的顶点。

悬挂边：与悬挂顶点关联的边，很像一根单股吊绳。

图G的最大度\(\Delta(G)\)：这个图里度数最大顶点的度。

无向简单最大度定理：设G为任意n阶无向简单图，则\(\Delta(G)\le n-1\)

图G的最小度\(\delta(G)\)：这个图里度数最小顶点的度。

在有向图中，顶点的度的概念仍然成立，不过新增了出度\(d^{+}(v)\)、入度\(d^{-}(v)\)、最大出度、最小出度、最大入度、最小入度，符号都懒得写了，具体含义也是很好理解的。

握手定理：在任何无向图中，所有顶点的度数之和等于边数的两倍；在任何有向图中，所有顶点的度数之和等于边数的两倍之外，所有顶点的出度之和和入度之和相等，都等于边数。

握手定理的推论：任何图（有向图和无向图）都有偶数个奇度顶点（因为度数之和是两倍，也就是偶数）。

图的度数列：

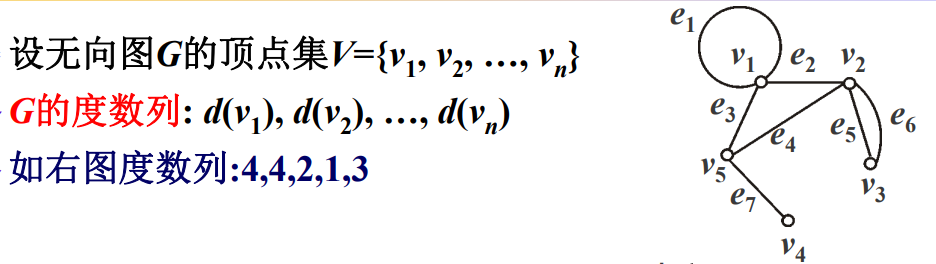
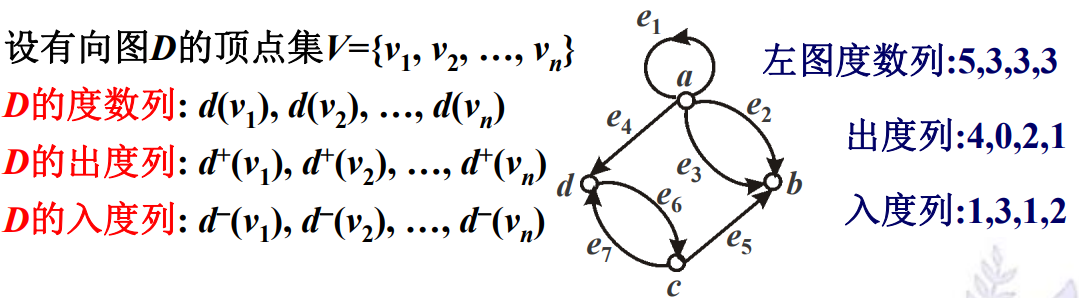
如果给一非负整数列d存在对应的以此为度数列的图，则称d是可图化的，如果所得图是简单图（没有平行边和环的图），则称d是可简单图化的。

可图化定理：如果非负整数序列d可图化当且仅当d元素之和为偶数。

同构：

设\(G_{1}=\left\langle V_{1}, E_{1}\right\rangle\)，\(G_{2}=\left\langle V_{2}, E_{2}\right\rangle\)为两个无向图（有向图），若存在双射函数\(f: V_{1} \rightarrow V_{2}\)，是的对于任意的\(v_{i}, v_{j} \in V_{1}\)，满足

\(\left(v_{i}, v_{j}\right) \in E_{1}\)（\(<v_{i},v_{j}>\in E_{1}\)）当且仅当\(\left(f\left(v_{i}\right), f\left(v_{j}\right)\right) \in E_{2}\)（\(<f(v_{i}),f(v_{j})>\in E_{2}\)）；

\(\left(v_{i}, v_{j}\right) \)（\(<v_{i},v_{j}>\)）与\(\left(f\left(v_{i}\right), f\left(v_{j}\right)\right)\)（\(<f(v_{i}),f(v_{j})>\)）的重数相同，

则称\(G_{1}\)和\(G_{1}\)是同构的，记作\(G_{1} \cong G_{2}\)。

图形化地看就是两个图去掉标定可以画成一模一样的。

两图同构的条件：

充要条件：图中结点和边分别存在着一一对应，且保持同样的关联关系。

必要条件：节点数目相同，边数相同，度序列相同。

完全图：

无向完全图：没对顶点之间都有一条边的无向简单图（没有平行边和环）。n阶无向完全图记作\(K_{n}\)，边数易得，最大度等于最小度。

有向完全图：每对顶点之间均有两条方向相反边的有向简单图。最大度等于最小度，最大出度等于最小出度等于最大入读等于最小入度。

N阶竞赛图：基图为无向完全图的有向图。

k-正则图：每个顶点度数均为k的无向简单图。

子图：设G=<V,E>, G'=<V',E'>是两个图(同为无向,或同为有向图)。

易得，点不完全相同的情况下，边是不可能完全相同的。

生成子图：点完全的子图。（边也是可以完全的）

导出子图：把已有点集V’所有能连的边都连上了，设母图为G，V'的导出子图记为G[V']。或者导出了E’和其所有关联点，E'的导出子图记为G[E']。

补图：两个图的点个数相同，把边不重复地按一定方式叠加到一起可以变成无向简单图，则这两个图互为补图。

自补图：两个互补的图同构。

无向图的添删操作：

G-e：从G删除e。

G-E'：从G删除E'中边。

G-v：从G删除v。

G-V'：从G删除V'中点。

G\e：从G中删除e后将e的两个断电用一个新的定点代替，成为收缩边e。

G+(u,v)：在G中u，v之间添加边（u，v）。

简单通路也叫迹。

通路和回路序列也可以“点边点边点……”表示，也可以只用边表示，在简单图中，甚至可以只用点表示。

在无向图中，长度为1的圈由环构成，长度为2的圈由两条平行边构成。在无向简单图中，所有圈的长度不小于3。在有向图中，长度为1的圈也由环构成。在有向简单图中，所有圈的长度不小于2.

不同的圈：定义意义下，无向图中长度为l（不小于3）的圈有2l个；有向图中长度为l（不小于3）的圈，有l个。在同构意义下，长度相同的圈均为1个。

初级通路（回路）是简单通路（回路），反之不一定。

通路长定理：在n阶图G中，若从顶点u到v（u不是v）存在通路，则u到v存在长度小于等于n-1的通路。

推论：在n阶图G中如果u到v（u不等于v）存在通路，则u到v一定存在长度小于等于n-1的初级通路。

回路长定理：在n阶图中, 若存在v到自身的回路, 则一定存在v到自身长度小于等于n的回路。

推论：在n阶图中, 若存在v到自身的简单回路, 则一定存在v到自身长度小于等于n的初级回路。

u与v连通：u与v之间有通路，记为u~v，规定u~u。可验证连通关系为等价关系。

连通图：任意两点都连通的图。规定平凡图是连通图。

非连通图：不是连通图的图。

形象地说就是只要能联通的一堆点就是一个连通分支，不能互相连通的k堆点就是k个连通分支。连通图的连通分支p(G)=1。

点到自身的距离为0。

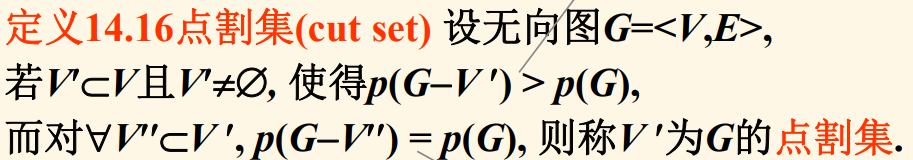
割掉能使连通分支增加的最小点集。

如果点割集里只有一个点，那么称那个点为割点。

边割集也是一样的道理。如果边割集里只有一条边，那么称那个边为割边或桥。

完全图是没有点割集的。

n阶零图点割集和边割集都没有。

连通图被边割集切割后连通分支数为2。

连通图被点割集切割后连通分支数大于等于2。

点连通度：使连通图G成为一个不连通图需要删去的点的最少数目（最小点割集点数），记为\(\kappa(G)\)。

边连通度：类似，记作\(\lambda(G)\)。

连通度不等式定理：对于任何无相连通图G，有\(\kappa(G) \leq \lambda(G) \leq \delta(G)\)。

有向图弱连通（连通）：基图为无向连通图。

有向图单向连通：任意两点必有一点可达另一点。

有向图强连通：任一点对相互可达。

强连通定理：D是强连通的当且仅当D中存在经过所有顶点的回路。

单向连通定理：D是单向连通的当且仅当D中存在经过所有顶点的通路。

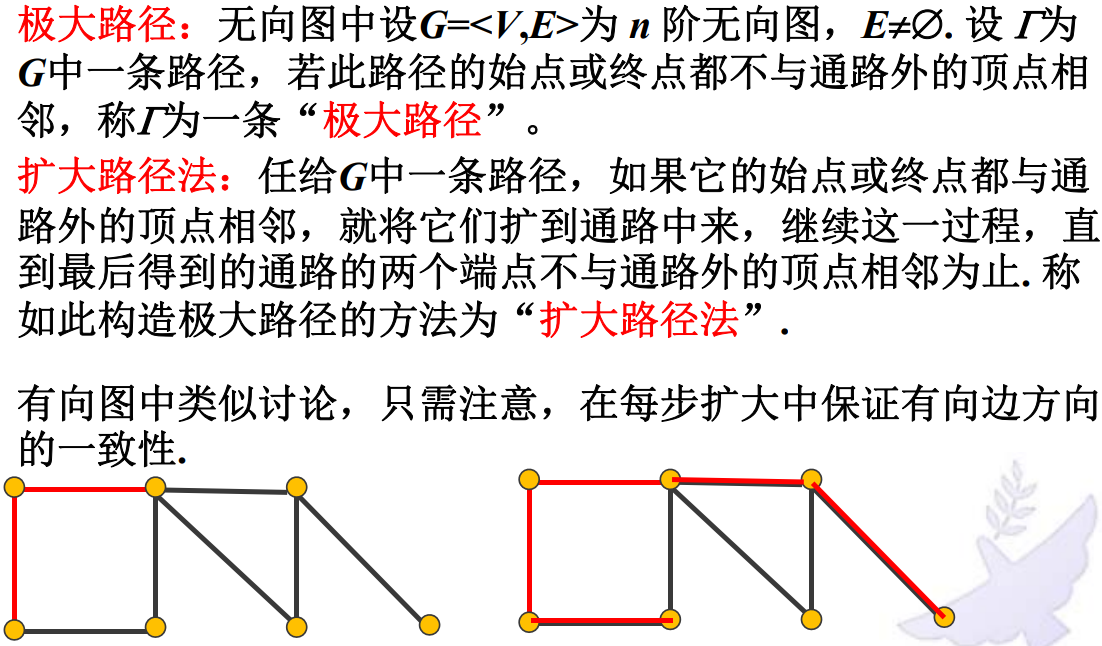
由某条路径扩大出的极大路径不唯一，极大路径不一定是图中最长的路径。

在完全图Kn中的极大路径是最长的路径，长度为n-1。

二部图：如果一个无向图中的点能够划分为两个点集，而图中所所有边的两个端点分别来自这两个点集，就称这个图为二部图（或称二分图、偶图等），记为\(G<V_{1},V_{2},E>\)。称那两个点集为互补顶点子集。

完全二部图：G是简单二部图，且任意一个点集中的任意一个点与另一个点集中的所有点相邻，记为\(K_{r,s}\)，r和s是两个点集的点数。

注意：n阶零图为二部图。

二部图判定定理：大于等于二的n阶无向图G是二部图当且仅当G中无奇圈。

同构图判定：最大圈法。

无向图的关联矩阵：矩阵的元素为点与边的关联次数，记为M(G)。

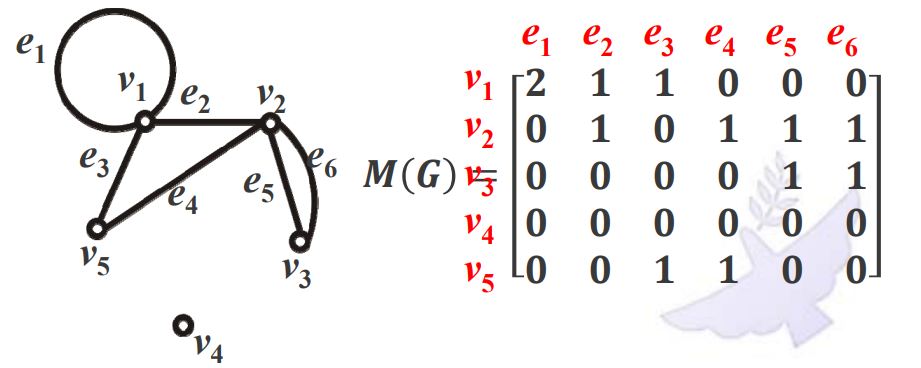
一行代表一个点，一列代表一个边。

无环有向图的关联矩阵：1代表始点，-1代表终点，0代表不关联，记为M(D)。

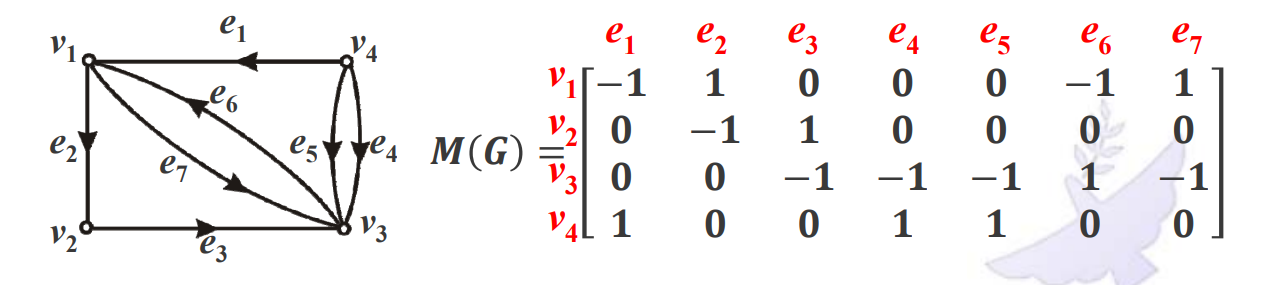
仍然是一行代表一个点，一列代表一个边。

有向图的邻接矩阵：行和列都代表点，矩阵元素是行中点邻接到列中点边的条数，记为A(D)，简记为A。

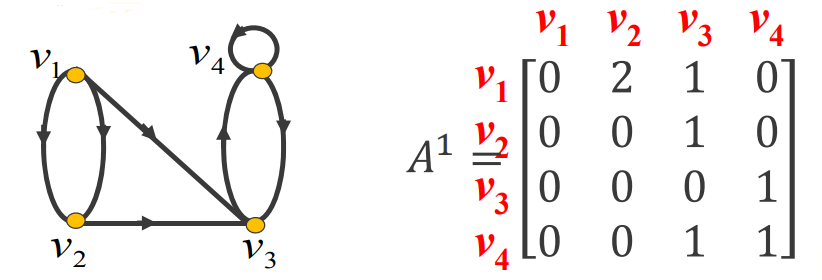
邻接矩阵的幂\(A^{l}\)：

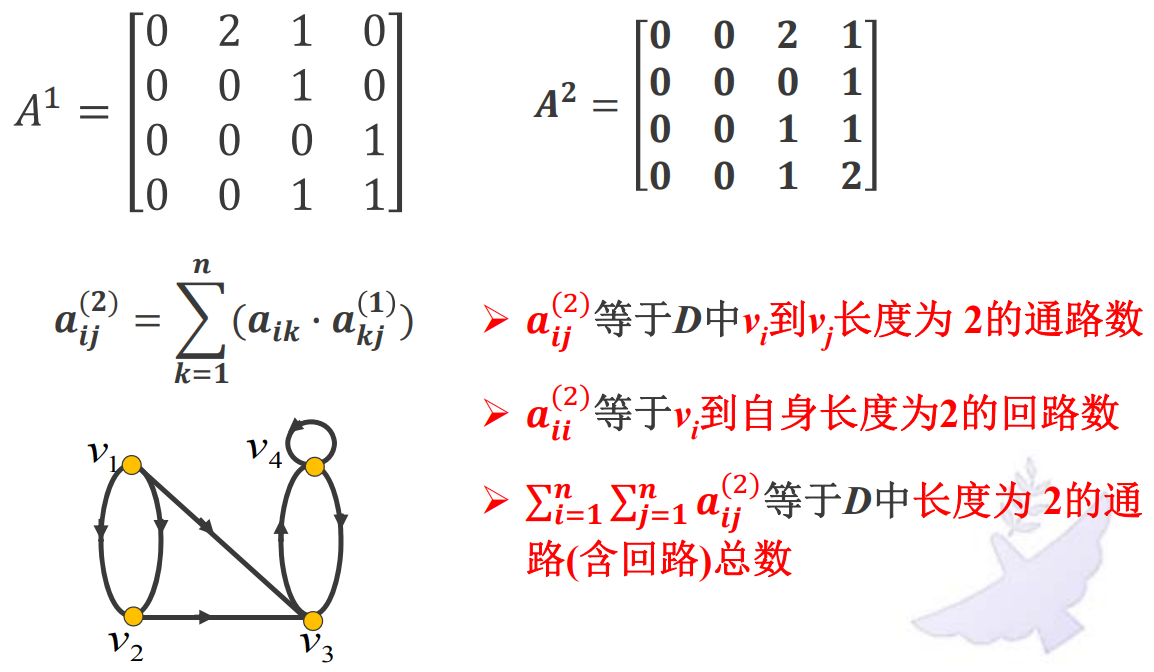
有向图中的通路数与回路数定理：

\(a_{ij}^{(l)}\)等于D中vi到vj长度为l的通路数。

\(a_{i}^{(l)}\)等于vi到自身长度为l的回路数。

\(\sum_{i=1}^{n} \sum_{j=1}^{n} a_{i j}^{(l)}\)等于D中长度为l的通路（含回路）总数。

\(\sum_{i=1}^{n} a_{i i}^{(l)}\)等于D中长度为l的回路总数。

上述结论稍加变通对无向图也成立。

有向图的可达矩阵：还是行和列都是点，行点可达列点则对应元素为1，否则为零，该矩阵记为P。

可达矩阵的求法：

图是不交的：两个图的点交集为空集。

图是边不交或边不重的：两个图的边交集为空集。

并图：以两个不含孤立点的图的点集的并集为点集，以其边集的并集为边集的图。

交图：以两个不含孤立点的图的边集的交集为边集，相关联的点组成点集的图。

差图：以两个不含孤立点的图的边差集为边集，相关联的点组成点集的图，记为\(G_{1}-G_{2}\)。

环合：先并图，再去掉重复边（也可理解为并图与交图的差图），记为\(G_{1} \oplus G_{2}\)。

欧拉图与汉密顿图

欧拉通路：经过图中每条边一次且仅一次行遍所有顶点的通路（点可以经过多次）。

欧拉回路：经过图中每条边一次且仅一次行遍所有顶点的回路（点可以经过多次）。

欧拉图（E图）：具有欧拉回路的图。

半欧拉图：具有欧拉通路而无欧拉回路的图。

说明：规定平凡图是欧拉图；欧拉通路是生成的简单通路（通路序列中所有边各异），欧拉回路是生成的简单回路；环不影响图的欧拉性。

欧拉图判定定理：无向图G是欧拉图当且仅当G连通且无奇度数顶点。

半欧拉图判定定理：无向图G是半欧拉图当且仅当G连通且恰有两个奇度顶点。（一笔画判定问题）

欧拉图圈判定定理：G是非平凡的欧拉图当且仅当G是连通的且为若干个边不重的圈之并。

有向欧拉图判定定理：有向图D是欧拉图当且仅当D是强连通的且每个顶点的入度都等于出度。

有向半欧拉图判定定理：有向图D是半欧拉图 当且仅当(1) D是单向连通的，(2) D中恰有两个奇度顶点，其中一个的入度比出度大1，另一个的出度比入度大1，而其余顶点的入度都等于出度。

Fleury算法求欧拉回路。

求欧拉回路算法：

哈密顿通路：经过图中所有顶点一次且仅一次的通路。

哈密顿回路：经过图中所有顶点一次且仅一次的回路（回来那次不算）。

哈密顿图（H图）：具有哈密顿回路的图。

半哈密顿图：具有哈密顿通路且无哈密顿回路的图。

说明：平凡图是哈密顿图；哈密顿通路是初级通路（所有顶点各异，所有边各异），哈密顿回路是初级回路；环与平行边不影响哈密顿性；哈密顿图的实质是能将图中所有顶点排在同一个圈上。

无向哈密顿图必要定理：无向图G是哈密顿图，对于该图点集的任何非空子集，把它去掉后图的连通分支数不大于这个子集的点数，即\(p\left(G-V_{1}\right) \leq\left|V_{1}\right|\)。

注意：因为是必要条件，所以不能用其判断无向哈密顿图，只能判断某无向图不是哈密顿图。

推论：设无向图G为版哈密顿图，对于任意非空的点集子集，均有\(p\left(G-V_{1}\right) \leq\left|V_{1}\right|+1\)

二部图关于哈密顿图的判定：

如果两个点集点数相同，则是哈密顿图。

如果两个点集点数相差1，则是半哈密顿图。

如果两个点集点数相差不小于2，则不是哈密顿图或半哈密顿图。

哈密顿通路充分定理：设G是n阶无向简单图，若对于任意不相邻的顶点u,v均有\(d(u)+d(v) \geq n-1\)，则G中存在哈密顿通路。

哈密顿图（哈密顿回路）充分定理：设G为n（n不小于3）阶无向简单图，若对于G中任意两个不相邻的顶点u, v均有\(d(u)+d(v) \geq n\)，则G中存在哈密顿回路，从而G为哈密顿图。

注意：都是充分条件，不满足该定理的图也有可能是哈密顿图。

哈密顿图充要定理：设u,v为n阶无向简单图G中两个不相邻的顶点，且\(d(u)+d(v) \geq n\)，则G为哈密顿图当且仅当\(G \cup(u, v)\)。

竞赛图哈密顿定理：大于等于二阶的竞赛图（基图为无向完全图的有向图）中都有哈密顿通路。

树

无向树：连通无回路的无向图。

平凡树：平凡图（一个点）。

森林：至少由两个连通分支（每个都是树）组成。

树叶：1度顶点。

分支点：度数不小于2的点。

注：这里所说的回路指初级回路或者简单回路。

树叶下限定理：T是n阶非平凡的无向树，则T中至少由两片树叶。

平面图

可平面图/平面图：能将G除顶点外无边相交地画在平面上。（可平面是一种“能力”，也就是说，只要“能”，即使表现出来的样子存在交点，也算平面图）

平面嵌入：画出的无边相交的平面图。

非平面图：无平面嵌入的无向图。

说明：一般所说的平面图不一定指平面嵌入，但在讨论某些性质时，一定是指平面嵌入；1~4阶完全图和5阶完全图减一条边都是平面图；有一组点集点数为2的完全二部图\(K_{2,n}\)也是平面图，\(K_{1,n}\)也是平面图；\(K_{5},K_{3,3}\)不是平面图。

平面图子母图定理：平面图的子图都是平面图。非平面图的母图都是非平面图。

平面复杂化定理：设G是平面图，则在G中加入平行边或环后所得的图还是平面图。

G的面：由G的平面嵌入的边将平面划分成的区域。

无限面/外部面（\(R_{0}\)）：面积无限的面。

有限面/内部面（\(R_{k}\)）：面积有限的面。

面\(R_{i}\)的边界：包围\(R_{i}\)的所有边组成的回路。

面\(R_{i}\)的次数：\(R_{i}\)边界的长度，用deg（\(R_{i}\)）表示。

面\(R_{i}\)的边界回路：可能是初级回路（圈）；可能是简单回路；可能是复杂回路；特别地，还可能是非连通回路之并（如\(R_{0}\)）。

次数和定理：平面图各面次数之和等于边数的两倍。

极大平面图：若在简单平面图G中的任意两个不相邻的顶点之间加一条新边所得图为非平面图，则称G为极大平面图。

若无不相邻顶点，那显然就是极大平面图了。

极大平面图特征定理：极大平面图是连通的，并且，3阶及以上极大平面图中没有割点和桥。

极大平面图判定定理：设G为不小于3阶的简单连通图，G为极大平面图当且仅当G的每个面的次数均为3。

极小非平面图：若在非平面图G中任意删除一条边，所得图G’为平面图，则称G为极小非平面图。

说明：极小非平面图必为简单图。

欧拉公式：设连通平面图G的顶点数、边数和面数分别为n，m和r，则n-m+r=2。

欧拉公式的推广：如果G有k个连通分支，那么n-m+r=k+1。

边顶点关系定理：设G为连通的平面图，且每个面的次数至少为l，（即\(deg(R_{i}) \geq l\)），\(l\geq 3\)，则G的边数m与顶点n有关系：\(m \leq \frac{l}{l-2}(n-2)\)。

推论：\(K_{5},K_{3,3}\)都是非平面图。

边顶点关系定理的推广：如果G有k个连通分支，那么\(m \leq \frac{l}{l-2}(n-k-1)\)

极大平面图边顶点关系定理：设G为n（n大于等于3）阶m条边的极大平面图，则m = 3n-6。

推论：如果上面的极大平面图改为简单平面图，则结论的等于号变为小于等于号。

简单平面图最小度定理：设G为简单平面图，则G的最小度不大于5。

注意：上面的一堆定理基本都是平面图的必要条件，不是充分条件，不能拿来判断图是否为平面图。

同胚：两图同构或者反复插入或消去2度顶点后同构。

平面图的判定充要定理1：当G中不含与\(K_{5}\)或\(K_{3,3}\)同胚的子图。

平面图的判定充要定理2：当G中无可收缩为\(K_{5}\)或\(K_{3,3}\)的子图。

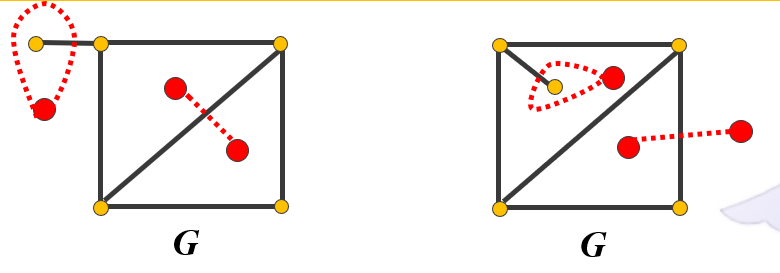
对偶图的性质：是平面图而且是平面嵌入；是连通图；与原图环对应桥桥对应环；多数情况下为多重图（含平行边的图）；同构的平面图（平面嵌入）对偶图不一定是同构的。

对偶图与原图的关系定理：对偶图的定点数等于原图的面数，对偶图的边数等于原图的边数，对偶图的面数等于原图的点数。

对偶图与原图的关系定理的推广：设原图有k个连通分支：对偶图的定点数等于原图的面数，对偶图的边数等于原图的边数，对偶图的面数等于原图的点数-k+1，设G*的顶点vi*位于G的面Ri中，则，\(d_{G^{*}}\left(v_{i}^{*}\right)=deg\left(R_{i}\right)\)。（deg：面边界的长度）

自对偶图：某个对偶图与其原图同构。

支配集、覆盖集、独立集、匹配与着色

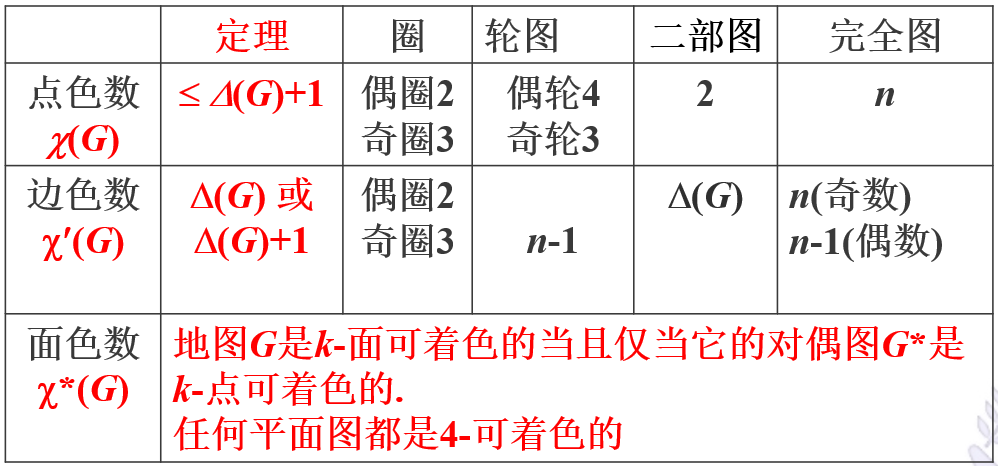
说明：色数为1的图是零图；完全图的色数等于阶数；偶圈的色数为2，奇圈的色度为3；奇阶轮图的色数为3，偶阶轮图的色数为4；色数为2当且仅当该图为二部图（至少有一条边）。

色数上界定理：对于任意无环有向图G，均有\(\chi(G) \leq \Delta(G)+1\)。

Brooks定理：若连通无向图不是完全图K也不是奇数阶的圈，则\(\chi(G) \leq \Delta(G)\)。

点着色法简介：

因为是贪心法，所以验证得到WelchPowell法不一定得到最优解。

地图：连通无桥平面图（嵌入）及其所有的面。

国家：地图的面。

两个国家相邻：它们的边界至少有一条公共边。

地图着色定理：地图G是k-面可着色的当且仅当它的对偶图G*是k-点可着色的。

四色定理：任何平面图都是4-可着色的。

Vizing定理：简单图的边色数只可能取两个值：图的最大度或图的最大度加一。

二部图边着色定理：二部图的边色数等于该图的最大度。

总结：

希望
你永远爱知识
纵使
命运不公
也要
保持纯洁
对文明传达来的
不死的
真理与探索欲
保持向往